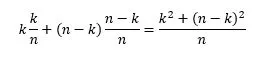In part 1 of this series, I described how I played the game "Guess Who" my six-year-old son Justus and we both got thinking about the kind of moves that would improve our chances of winning. Before I get any deeper into the topic, let me ask the question: How and why does this strategy work?
A little bit of probability theory can help us to understand why this strategy works. When I ask a particular yes-no question, I can use the following formula to work out the "expected value" when the question has been answered:
Where n is the total number of cards and k is the number of cards to which the answer "yes" applies. In both cases, you mustn't count the card that your opponent has to guess. To calculate the expected value, we assume that all the remaining cards have an equal probability of being the one we are looking for. As this card was taken purely at random from a deck of cards at the beginning, this is a reasonable assumption. A little less obvious is whether it's really enough just to look at the next question, or whether you'd fare a little better by calculating all the remaining moves through till the end of the game. I'll leave that question open for now – but I'd be happy to hear your thoughts.
What we want is, of course, to have as few cards as possible left after our question has been answered. We therefore need to ask a question for which the expected number, as explained earlier, is as small as possible. The value n is the same for all questions (in the same round of the game); only the value k is different. So which values for k will give us the smallest expected value? A bit of curve discussion will help us out here. The second derivative of the above expected value after k is constant at 4/n, i.e. it is always positive. So if we find a zero of the first derivative, we have found our minimum. The first derivative is 4k/n-2; so the zero is k=1/2 n. If this cannot be met exactly because there is no suitable question, you have to choose a question that keeps the difference between k and 1/2 n is as small as possible. This fits perfectly with the strategy we described earlier. You could also look at it like this: choose the question for which the smaller of the two numbers k and n-k is as big as possible.
If you're not a fan of derivatives, you can of course plot the expected value function for different values of n to find the minimum, which is slightly less rigorous but perhaps easier to understand. The result is a nice parabola, as you can see for the example of n = 10 here with the help of Wolfram Alpha. You could, of course, do the same thing with paper and pencil.
Programming for young data science enthusiasts: an overview of a game strategy
It has to be admitted that counting the cards for every question is a lot of effort. Wouldn't it be nice to know once and for all what questions to ask? This is not entirely possible, however, because, as we have seen, the card your opponent has to guess also influences matters. But if we simply choose to ignore it, we could draw up an effective gaming strategy on paper in the form of a tree.
Because data science always includes data (which might sound ridiculously obvious, but in practice is not always understood by everyone) and, of course, a bit of program code, this is probably a good time to make use of both. So we'll write a small program to calculate and output a game tree. The source code is available here, but if you prefer, you can try the notebook in Google Colab directly without the need to carry out an installation (see the link at the top of the notebook). If you want to try the program on your own device, however, you'll need to install graphviz to process the nice tree graphics, and that might be a bit tedious.
Our data is small and manageable. It is a matrix with the questions in the columns and the characters (cards) in the rows. A matrix entry is exactly 1 if the answer to the question is "yes". Otherwise, it's 0. The matrix is so small (24 rows and 15 columns) that we simply define it inside the notebook without having to move it to an external file.

If you look at the totals for each column of the matrix, you'll see the number of cards for which a specific question is answered with "yes". And here comes the first surprise: contrary to what is stated in the German Wikipedia article, the questions do not all have exactly five cards with "yes" answers. The biggest difference is in the cards of faces with a beard, which are eight in number. There are other cards with four yes answers, namely the chin beard and the brown hair color. The English Wikipedia entry makes no mention of these five yes-answers, by the way.
To save the game tree, I use the handy Python Anytree package, which is a very easy way of generating a tree data structure. The package also offers nice visualization options via graphviz.
The game-tree class then brings together everything we need to create the game tree. Most of the work is done in the generate_tree method. It figures out the correct question according to the counting method described earlier and then calls itself again to determine the correct question for the two possible answers (yes and no). While doing so, it saves the intermediate results of each calculation in the game tree. When there is only one card left, the recursion is terminated.
When I say "the right question", I appreciate that this is somewhat inexact because sometimes there's more than one question with the highest possible lucky number. In that case, the program simply selects one of them at random (the first one it has calculated). So the solution it offers is not necessarily the only possible one. There are others that are just as good.
The generated tree has some interesting characteristics. The root node tells us that it's a good idea to ask about a beard first. This advice doesn't change, by the way, even if you take into account the mystery card you are holding. The question about the beard is always the best first question. This is because its lucky number at the beginning of the game is 8 (8 "yes" answers and 16 "no" answers), while all other questions have a lucky number no bigger than 5. So even if the lucky number is reduced by one, it's still bigger than the number for all the other questions.
(Tip: Click on the picture to make it larger)
More fun and games with "Guess Who?"
If you make use of the tree when you play the game, the total number of questions you'll need to ask will vary between four and six. There is an average of 4,625 questions, which is very close to information theory's lower bound of around 4.58 (binary logarithm of 24). There is no strategy that is able to reduce the number of questions to just four. But is there one that never needs more than five? I'd love to hear your thoughts on that.
Different versions of the game have been released over the years, such as travel versions with only twenty cards, different editions with different faces, and even a version with animals. If you have a different version than the one on my photo (which is from my wife's childhood), please adapt the program to suit your version. I look forward to hearing how you get on.