Im ersten Teil unserer Serie haben wir uns angeschaut, wie die Bayes-Statistik genutzt werden kann, um den Bedarf an Trainingsdaten beim bestärkenden Lernen zu verringern. In diesem Artikel wollen wir diese Idee mithilfe von TensorFlow Probability, einem brandneuen Tool von Google, in ein kleines Modell umsetzen.
Schere, Stein, Papier
Schere, Stein, Papier ist sicherlich eines der einfachsten Spiele überhaupt. Dennoch findet man im Internet eine erstaunliche Menge an Literatur dazu. Wir wollen die Bayes-Statistik nutzen, um dieses Spiel zu spielen und dabei die Ungleichgewichte auszunutzen, denen menschliche Entscheidungen unterworfen sind. Dazu entwickeln wir ein Modell von der Denkweise unseres Gegners und wählen anschließend einen Spielzug, mit dem wir ihn schlagen können. Die wichtigsten Abschnitte unseres Codes werden in diesem Artikel dargestellt und erläutert. Der komplette Code zum Selbstausprobieren findet sich im vollständigen Notebook. Um unser Modell möglichst einfach zu halten, konzentrieren wir uns auf das einfachste Ungleichgewicht: Wir wollen Unterschiede in den Häufigkeiten modellieren, mit denen ein menschlicher Spieler sich für einen der drei Spielzüge entscheidet.
Ein Modell erzählt, wie die Daten entstanden sein könnten
Eines der schönsten Merkmale der Bayes-Methode besteht darin, dass man ein Modell erstellen kann, indem man einfach nur den Prozess der Datengenerierung Schritt für Schritt beschreibt.
Probieren wir das einmal für unser Spiel:
- Irgendwo tief im Innern eines menschlichen Kopfes verbirgt sich eine geheime Wahrscheinlichkeitsverteilung über die drei Spielzüge Schere, Stein und Papier.
- Anhand dieser Wahrscheinlichkeitsverteilung trifft unser menschlicher Gegner seine Wahl.
- Dieser Prozess wiederholt sich in jeder Runde, wobei wir die Häufigkeit von Schere, Stein und Papier zählen. Diese Daten wollen wir nutzen, um die geheime Wahrscheinlichkeitsverteilung offenzulegen.
Wenn wir das jetzt in ein Modell übersetzen, ist es am einfachsten, mit dem letzten Schritt zu beginnen, weil er sich auf die konkreten Daten bezieht, die wir nutzen wollen. In unserem Fall handelt es sich um sehr simple Daten: Es wird lediglich gezählt, wie häufig sich unser menschlicher Gegner bisher für Schere, Stein bzw. Papier entschieden hat.
Zieht man aus einer Urne, die verschiedenfarbige Kugeln enthält, eine Kugel heraus, legt sie zurück und wiederholt mehrmals, so folgt die Anzahl der Kugeln jeder Farbe der sogenannten Multinomialverteilung. Wenn wir also behaupten, dass die Anzahlen der drei Spielzüge aus einer Multinomialverteilung gezogen werden, bedeutet das nur, dass sich die Spielzüge ebenso verhalten wie die Kugeln im Urnenexperiment. Das bedeutet auch, dass jede Spielrunde unabhängig von allen anderen Runden ist. Ein menschlicher Spieler wendet häufig Strategien an, die Abhängigkeiten zwischen den Runden schaffen, indem er sich beispielsweise scheut, einen bestimmten Spielzug häufiger als zwei- oder dreimal hintereinander zu wählen. Wir wissen also schon, dass die Unabhängigkeit nicht immer gegeben sein wird. Sie kann dennoch eine sinnvolle Annahme sein, wenn sie es uns ermöglicht, gut zu spielen.
Jetzt wird’s bayesianisch
Bisher ist nichts an unserem Modell spezifisch bayesianisch. Die Verwendung einer Multinomialverteilung in diesem Kontext versteht sich für jeden Statistiker quasi von selbst – sogar für diejenigen, die sich vehement von Bayes-Ansätzen distanzieren.
Genuin bayesianisch ist der nächste Schritt, bei dem wir festlegen müssen, welches Vorwissen in Bezug auf die Wahrscheinlichkeit von Schere, Stein und Papier wir in unser Modell integrieren möchten. Dazu legen wir eine Wahrscheinlichkeitsverteilung fest, die verschiedene Kombinationen von Wahrscheinlichkeiten für Schere, Stein und Papier liefert. Dafür eignet sich die sogenannte Dirichlet-Verteilung. Wenn Sie davon zum ersten Mal hören – keine Sorge. Für unsere Zwecke genügt es, zu wissen, dass wir die Version mit drei Parametern nutzen und dass jeder der drei Parameter einem möglichen Spielzug entspricht: Schere, Stein oder Papier. Ist einer der Parameter (z. B. für Papier) größer als ein anderer (z. B. für Stein), dann wird Papier mit höherer Wahrscheinlichkeit auftreten als Stein. Sind alle drei Parameter gleich eins, wird aus der Dirichlet-Verteilung eine Gleichverteilung. Diesen Fall werden wir für die A-priori-Verteilung nutzen. Das bedeutet, dass wir nicht wissen, welcher Spielzug mit einer höheren Wahrscheinlichkeit auftritt als ein anderer, weshalb wir konsequenterweise eine sogenannte nichtinformative A-priori-Verteilung verwenden, die keine der drei Möglichkeiten bevorzugt.
Damit ist unser Modell fertig. Es besteht aus zwei Schritten: Im ersten Schritt werden die Wahrscheinlichkeiten für Schere, Stein und Papier aus einer Dirichlet-Verteilung gezogen, und im zweiten Schritt werden diese Wahrscheinlichkeiten in einer Multinomialverteilung eingesetzt, die die jeweilige Anzahl für jeden der drei Spielzüge generiert.
Das Modell in Code übersetzen
Wenn wir die Ideen aus dem vorherigen Abschnitt in Code übersetzen, sieht das Ergebnis so aus.
joint_log_probability.py
# We calculate the joint log probability.
# It answers the big and central question in each Markov chain simulation: What's the probability
# that this data occurs together with these distribution parameters?
@tf.function(input_signature=5 * (tf.TensorSpec(shape=[], dtype=tf.float32),))
def joint_log_prob(total_rock, total_paper, total_scissors, p_rock, p_paper):
'''
Joint log probability of data occuring together with given parameters.
:param total_rock: number of rock occurences
:param total_paper: number of paper occurences
:param total_scissors: number of scissors occurences
:param p_rock: probability of rock
:param p_paper: probability of paper
'''
total_count = total_rock + total_paper + total_scissors
# Start by defining a prior for the rock / stone / scissor outcomes.
# The three parameters are proportional to the prior probabilities of rock, paper, and scissors, respectively.
# We want to start with a situation in which all combinations of probabilities for
# rock/paper/scissors are equally likely.
# Dirichlet is the analogue of having a beta prior in the case of only two options instead
# of three. In particular, Dirichlet([1, 1]) is a uniform distribution.
rv_rsp_prior = tfd.Dirichlet([1., 1., 1.], name='rv_rsp_prior')
rv_rsp_outcomes = tfd.Multinomial(total_count=total_count, probs=[p_rock, p_paper,
tf.constant(1., tf.float32) - p_rock - p_paper],
name='rv_rsp_outcomes')
# calculate prior log probability of parameters
joint_log_prob = rv_rsp_prior.log_prob([p_rock, p_paper, tf.constant(1., tf.float32) - p_rock - p_paper])
# add log likelihood of data
joint_log_prob = tf.add(joint_log_prob, rv_rsp_outcomes.log_prob([total_rock, total_paper, total_scissors]))
return joint_log_prob
Als Erstes fällt vielleicht auf, dass wir hier keine Wahrscheinlichkeit berechnen, sondern den Logarithmus einer Wahrscheinlichkeit. Das hat rein numerische Gründe: Die Wahrscheinlichkeiten, mit denen wir arbeiten, fallen in manchen Fällen so winzig aus, dass numerische Probleme auftreten können. Verwenden wir stattdessen Log-Wahrscheinlichkeiten, können wir den verfügbaren Zahlenbereich einer Gleitkommazahl besser ausnutzen, sodass numerische Probleme sehr viel unwahrscheinlicher werden. Log-Wahrscheinlichkeiten sind genauso einfach zu benutzen wie die Wahrscheinlichkeiten selbst. Man muss lediglich immer dann, wenn man Wahrscheinlichkeiten multiplizieren würde, die entsprechenden Log-Wahrscheinlichkeiten addieren.
Unser wesentliches Ziel in diesem Schritt besteht darin, eine Funktion zu schreiben, die die gemeinsame Log-Wahrscheinlichkeit eines Datenpunktes (d. h. drei Zahlen, jeweils eine für Schere, Stein und Papier) und die entsprechenden Parameterwerte (hier reichen die Wahrscheinlichkeiten für Stein und Papier, aus denen sich die Wahrscheinlichkeit für Schere dann ergibt) ausgibt. Der Rest ist einfach: Wir verwenden die Dirichlet-Verteilung für die Berechnung der Log-Wahrscheinlichkeit unserer Wahrscheinlichkeitsparameterwerte und die Multinomialverteilung für die Berechnung der Log-Wahrscheinlichkeit der Anzahlen für Schere, Stein und Papier. Anschließend addieren wir die beiden Log-Wahrscheinlichkeiten und erhalten die gemeinsame Log-Wahrscheinlichkeit dafür, dass diese Anzahlen gemeinsam mit diesen Wahrscheinlichkeitsparametern (p_rock und p_paper) auftreten. Fertig! Wir haben unser Bayes-Modell in Code übersetzt.
Schätzung der Parameterwerte
Ich habe gerade behauptet, dass unser Modell fertig sei. Wie aber schätzt man die Parameter des Modells (insbesondere p_rock und p_paper), wenn man lediglich ein paar Daten und eine Funktion für die gemeinsame Log-Wahrscheinlichkeit hat? Glücklicherweise ist in TensorFlow Probability für genau diese Aufgabe eine ziemlich raffinierte Maschinerie eingebaut. Sie nennt sich Markov-Chain-Monte-Carlo, und wir wenden die neueste und beste Variante dieser Methode an, die auf den Namen Hamilton-Monte-Carlo hört. Damit können wir Stichproben aus der A-posteriori-Verteilung unseres Modells ziehen – also von der Verteilung, die wir von der A-priori-Verteilung ableiten, indem wir aus den beobachteten Anzahlen von Stein, Schere und Papier lernen. Ist unsere Stichprobe groß genug, erfahren wir alles, was wir über die Verteilung wissen müssen: die Form, den Durchschnitt, den Median, die Modi usw. Hamilton-Monte-Carlo zählt zu den Verfahren, die ziemlich verrückt klingen, bis man feststellt, wie gut sie funktionieren. Die intuitive Idee besteht darin, dass man sich die Verteilung, aus der man Stichproben ziehen möchte, als eine hochdimensionale Landschaft aus Bergen (hohe Wahrscheinlichkeit) und Tälern (geringe Wahrscheinlichkeit) vorstellt. Nun lässt man eine Kugel über diese Landschaft rollen. Überall dort, wo sie entlangrollt, zieht sie in regelmäßigen Zeitabständen Stichproben aus der Verteilung. Da die Kugel bergab an Fahrt gewinnt, rollt sie in den Tälern jedoch deutlich schneller – und zieht dort weniger Stichproben – als auf den Bergen. Überraschenderweise lässt sich das so umsetzen, dass es funktioniert. Wer mehr zu diesem Thema wissen möchten, dem seien Jeremy Kuns großartige Einführung in das Thema Markov-Chain-Monte-Carlo und der Blog-Artikel von Richard McElreath zu Hamilton-Monte-Carlo empfohlen. In unserem Fall ist es dieser Code-Schnipsel, der die Stichprobenziehung mithilfe von Hamilton-Monte-Carlo durchführt:
hamilton_monte_carlo.py
# observed data
total_rock = tf.constant(5., tf.float32)
total_paper = tf.constant(0., tf.float32)
total_scissors = tf.constant(0., tf.float32)
# define some constants
number_of_steps = 10000
burnin = 5000
# Set the chain's start state
initial_chain_state = [
1/3 * tf.ones([], dtype=tf.float32, name="init_p_rock"),
1/3 * tf.ones([], dtype=tf.float32, name="init_p_paper")
]
# for trainsforming contrained parameter space (in this case, [0, 1] for each parameter) to unconstrained real numbers
unconstraining_bijectors = [
tfp.bijectors.Sigmoid(), # bijector for p_rock
tfp.bijectors.Sigmoid() # bijector for p_paper
]
# fix data to the actually observed values in the joint log prob to optimize only over the unkown model parameters,
# and convert to tensorflow function for speedup
joint_log_prob_for_opt = tf.function(func=lambda x, y: joint_log_prob(total_rock=total_rock,
total_paper=total_paper,
total_scissors=total_scissors,
p_rock=x, p_paper=y),
input_signature=2 * (tf.TensorSpec(shape=[], dtype=tf.float32),)
)
# define the Hamilton markov chain by successively adding wrappers to an inner kernel
kernel = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=joint_log_prob_for_opt,
num_leapfrog_steps=2,
step_size=tf.constant(0.5, dtype=tf.float32),
state_gradients_are_stopped=True
)
kernel=tfp.mcmc.TransformedTransitionKernel(
inner_kernel=kernel,
bijector=unconstraining_bijectors
)
kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=int(burnin * 0.8)
)
# sample from the chain
[
posterior_p_rock,
posterior_p_paper
], kernel_results = tfp.mcmc.sample_chain(
num_results=number_of_steps,
num_burnin_steps=burnin,
current_state=initial_chain_state,
trace_fn=lambda _, kernel_results: kernel_results.inner_results.inner_results.is_accepted,
kernel=kernel)
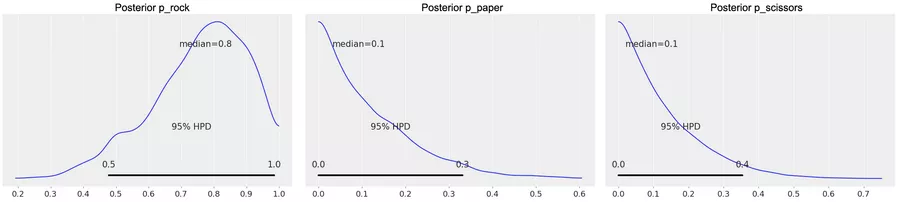
Zunächst legen wir beispielhaft die beobachteten Daten fest, an die wir das Modell anpassen wollen. In unserem Fall ist das fünfmal „Stein“, während „Schere“ und „Papier“ kein einziges Mal gewählt wurden. Anschließend bereiten wir die Markov-Kette technisch vor und ziehen dann Stichproben daraus. Wenn wir die Verteilung der Stichproben für p_rock graphisch darstellen (Abbildung 1, links), sehen wir, dass der Median bei 0,8 liegt, was bei fünfmal Stein und keinem einzigen Mal Schere und Papier sehr plausibel ist. Der Graph zeigt auch, dass es in Bezug auf den genauen Wert von p_rock noch einige Ungewissheit gibt. Die Graphen für p_paper und p_scissors (Abbildung 1, Mitte und rechts) zeigen, dass diese Werte wie erwartet sehr nahe an null liegen. Diese Werte könnten wir jetzt direkt für das bestärkende Lernen nutzen. Doch zunächst wollen wir überprüfen, ob unsere Simulation funktioniert hat.
Abbildung 1
TensorFlow 2 mit TensorFlow Probability
Wer die Markov-Chain-Simulation ausprobiert hat, stellt fest, dass es rund 17 Minuten dauert, um die entsprechende Zelle im Notebook auszuführen. Das liegt daran, dass der Code im Modus Eager Execution ausgeführt wird. TensorFlow 2 bietet alternativ auch Ausführungsmechanismen, die so ähnlich funktionieren wie der Graph-Modus in TensorFlow 1. Ich konnte jedoch nicht herausfinden, wie man sie mit TensorFlow Probability kombinieren kann, um die Markov-Chain-Simulation zu beschleunigen. Eigentlich sollte es reichen, wie in unserem Notebook tf.function zu verwenden (einmal als Decorator und einmal als Funktion). Leider bringt das keine Verbesserung der Performance. Derselbe Code (mit kleinen Änderungen für den Graph-Modus) wird in TensorFlow 1 etwa zehnmal schneller ausgeführt. Ich gehe davon aus, dass das Problem demnächst gelöst wird. Über entsprechende Ideen von Lesern (und Leserinnen!) freue ich mich. Möglicherweise müssen wir uns auch einfach bis zur nächsten Version von TensorFlow Probability gedulden. Bis dahin nehme ich lieber die schlechte Performance in Kauf, als das Notebook in TensorFlow 1 zu präsentieren, das sehr bald überholt sein wird.
Unsere Ergebnisse mathemagisch überprüfen
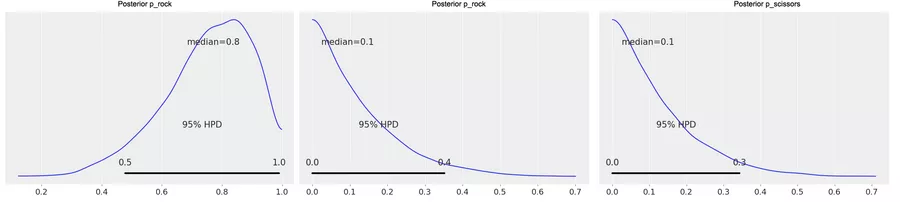
Da wir diese große Blackbox namens Hamilton-Monte-Carlo zum ersten Mal angewendet haben, ist es besser, wenn wir prüfen, dass sie auch die richtigen Ergebnisse generiert. Zum Glück befinden wir uns in einer außergewöhnlichen Situation: Normalerweise braucht man für die Parameterschätzung in Bayes-Modellen numerische Verfahren wie Hamilton-Monte-Carlo. Da wir unser Beispiel jedoch sehr simpel gehalten haben, befinden wir uns in der äußerst seltenen Situation, für die Parameterschätzung eine einfache mathematische Formel zur Verfügung zu haben. Damit können wir die Monte-Carlo-Ergebnisse ganz einfach überprüfen: Wenn wir eine A-priori-Dirichlet-Verteilung mit den Parametern (1, 1, 1) und den Daten (s, r, p) haben (wobei s/r/p die beobachteten Anzahlen von Schere/Stein/Papier sind), ist die entsprechende A-posteriori-Wahrscheinlichkeit (die Verteilung, aus der wir mithilfe von Hamilton-Monte-Carlo Stichproben gezogen haben) eine Dirichlet(1 + r, 1 + p, 1 + s)-Verteilung. Wenn man die entsprechenden Graphen der A-posteriori-Verteilung (Abbildung 2) mit Abbildung 1 vergleicht, stellt man fest, dass sie einander sehr ähnlich sind.
Abbildung 2
Spiel und Spaß mit bestärkendem Lernen
Nun ist es an der Zeit, unser Modell mithilfe von bestärkendem Lernen in ein Spiel zu verwandeln. Da das Spiel mehr Spaß macht, wenn die Spielzüge schnell berechnet werden, verwenden wir die „mathemagische“ Abkürzung aus dem letzten Abschnitt für die Berechnung der A-posteriori-Verteilung. Dieser Schnipsel enthält den Hauptteil des Codes.
main_game_code.py
class ButtonReaction():
def __init__(self, moves_widget, game_statistics_widget, plot_widget, show_plot):
self.moves = moves_widget
self.game_statistics = game_statistics_widget
self.plot = plot_widget
self.history = {'rock': 0, 'paper': 0, 'scissors': 0} # initialize history of moves of our human opponent
self.wins = [0, 0, 0]
self.show_plot = show_plot
def on_button_clicked(self, button_info):
actual_human_move = button_info.description.lower()
self.history[actual_human_move] += 1
history_list = [val for (key, val) in self.history.items()]
history_list_plus_one = [val + 1 for val in history_list] # compute parameters for Dirichlet distribution
no_rounds = sum(history_list)
probs = tfp.distributions.Dirichlet(history_list_plus_one).sample()
hypothetical_human_move = list(tfp.distributions.Multinomial(total_count=1, probs=probs).sample().numpy())
if hypothetical_human_move == [1.0, 0.0, 0.0]:
our_move = 'paper'
elif hypothetical_human_move == [0.0, 1.0, 0.0]:
our_move = 'scissors'
else:
our_move = 'rock'
if actual_human_move == our_move:
result = 'draw'
self.wins[2] += 1
if (actual_human_move, our_move) in [('rock', 'paper'), ('paper', 'scissors'), ('scissors', 'rock')]:
result = 'computer wins'
self.wins[1] += 1
else:
result = 'you win'
self.wins[0] += 1
if self.show_plot:
p_exact_posterior = tfp.distributions.Dirichlet(history_list_plus_one).sample(10000)
plot_probs = pd.DataFrame({'p_rock': p_exact_posterior[:, 0].numpy(), 'p_paper': p_exact_posterior[:, 1].numpy(),
'p_scissors': p_exact_posterior[:, 2].numpy()})
self.plot.clear_output(wait=False)
with self.plot:
fig, ax = plt.subplots()
ax.set_yticklabels(labels='') # the y-axis-labels are the concrete counts of rock/stone/scissors
# which are irrelevant here, so we switch y-axis-labels off
plot_probs.plot.kde(alpha=0.5, fig=fig, ax=ax)
show_inline_matplotlib_plots()
moves.value = f"result in round {no_rounds}: your move is {actual_human_move}, computer's move is {our_move}, {result}"
game_statistics.value = f'you won {self.wins[0]} times, computer won {self.wins[1]} times and we had {self.wins[2]} draws'
Er wird vom UI-Code aufgerufen, sobald wir im Spiel einen der Buttons betätigen. Das Argument „button_info“ ist entweder Schere, Stein oder Papier. Wer das Spiel beim Lesen ausprobieren möchte, kann dazu wieder das vollständige Notebook benutzen.
Das Spiel benutzt unser Modell, um herauszufinden, wie hoch die Wahrscheinlichkeit jeweils ist, dass sich unser menschliche Gegner für einen der drei Spielzüge entscheidet. Die Spielzugdaten und die daraus berechneten Wahrscheinlichkeiten werden nach jeder Runde aktualisiert. Anschließend ziehen wir aus dieser Verteilung den Spielzug, den unser Gegner wahrscheinlich wählen wird, und berechnen daraufhin unseren eigenen Spielzug: Entscheidet sich unser Gegner für Stein, wählen wir Papier. Wählt er Papier, entscheiden wir uns für Schere usw. Auf diese Weise entwickeln wir eine randomisierte Strategie, die genau widerspiegelt, wie häufig unser Gegner jedes Symbol wählt. Diese Strategie verwendet nicht nur einen Punktschätzer, sondern eine vollständige Verteilung der Wahrscheinlichkeit jedes einzelnen Spielzugs. Man kann sehen, wie sich diese Verteilung im Spielverlauf verändert. Dargestellt wird sie in einem kleinen Graphen, der nach jedem Spielzug aktualisiert wird. Es ist interessant, diese Änderungen zu beobachten, aber gleichzeitig verleihen sie dem menschlichen Gegenspieler einen unfairen Vorteil. Deshalb lassen sie sich abschalten, indem man am Anfang der Zelle „show_plot = False“ setzt.
Wie geht es weiter?
Wer bis hierher gelesen hat, mag (im besten Fall) den Eindruck gewonnen haben, dass die Bayes-Statistik und die Markov-Chain-Monte-Carlo-Methode spannend und nützlich sind. Vermutlich ist da auch ein Gefühl, dass ich viele wichtige Details übersprungen habe (was definitiv zutrifft). Um die Lücken zu schließen, gibt es einige hervorragende Bücher, die ich nur empfehlen kann: Einen tollen Einstieg ins Thema für Programmierer bietet Cam Davidson-Pilons „Bayesian Methods for Hackers“. Das Buch ist kostenlos auf Github verfügbar, und alle Beispiele wurden kürzlich in TensorFlow Probability übertragen. Wer sich eine eher statistisch geprägte Perspektive wünscht, dem sei „Statistical Rethinking“ von Richard McElreath ans Herz gelegt. Die Beispiele wurden (noch?) nicht in TensorFlow Probability übersetzt; lesenswert ist das Buch dennoch. Richard McElreath erklärt Konzepte auf klare und einfache Weise, die esoterisch anmuten, wenn man anderswo darüber liest. An dieser Stelle müsste ich eigentlich auch Literatur zum Thema bestärkendes Lernen empfehlen, doch leider bin ich noch auf kein Buch gestoßen, das mir so gefällt wie die beiden anderen Titel. Deshalb bin ich gespannt, was Ihre Lieblingsbücher zum Thema sind und welche Abenteuer Sie bei eigenen Experimenten mit Bayes-Statistik und bestärkendem Lernen erleben. Für Fragen, Kommentare und Anregungen bin ich jederzeit dankbar.